使用 CUDA 优化 KNN 求解
post on 07 Jul 2020 about 11642words require 39min
CC BY 4.0 (除特别声明或转载文章外)
如果这些文字帮助到你,可以请我喝一杯咖啡~

计算高维空间中的最近邻(nearest neighbor)
- 输入:查询点集,参考点集,空间维度
- 输出:对每个查询点,输出参考点集中最近邻的序号
实验中分别针对 CPU、GPU、多 GPU 三种计算环境上实现了上述实验要求,并实现了若干种优化版本进行对比,同时也使用空间划分结构 KD-Tree 对查询进行加速。实验使用 TA 提供的八组测试数据和自己构造的四组更大的测试数据对各个版本进行 benchmark 测试,并从结果分析得到了一些影响本次程序性能的因素。
如果要运行我的实验程序,可以终端直接在当前目录运行如下指令:
1
2
#chmod 777 ./RUNME.sh # 可用于解决有时出现文件权限错误的问题
./RUNME.sh | tee screen.log
该条语句会自动编译并运行实验程序,同时保存屏幕日志到 screen.log 文件中。我的运行结果可以直接看当前目录下的 screen.log。
介绍程序整体逻辑,包含的函数,每个函数完成的内容。对于核函数,应该说明每个线程块及每个线程所分配的任务
我分别实现了串行的 v0 版本、 基于 CUDA 的 v1~v8 版本、使用 CPU 上的 KD-Tree 的 v9 版本、使用 GPU 上的 KD-Tree 的 v10 版本。如下,如果要在它们之间进行切换,只需要修改 sources/src/core.cu 最后几行 cudaCallback 函数中实际调用的版本即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void cudaCallback(
int k,
int m,
int n,
float *searchPoints,
float *referencePoints,
int **results)
{
v8::cudaCallback(
k,
m,
n,
searchPoints,
referencePoints,
results);
}
v0
v0 版本是 TA 提供的串行版本,用于检验运行结果的正确性。其逻辑如下:
- 枚举查询点集所有的点
- 设查询点下标
mInd - 初始化当前最优距离为无穷大
- 枚举参考点集所有点
- 设参考点下标
nInd - 计算查询点和参考点的距离
- 为了减少一次不必要的开方运算,这里保存的是距离的平方
- 若查询点到参考点距离比当前最优距离更优
- 更新当前最优距离
- 记录当前参考点坐标
nInd
- 设参考点下标
- 保存最优参考点下标到答案向量中
- 设查询点下标
- 返回结果
v0 版本中仅有一个 cudaCallback 函数作为外部调用的接口。
v1
v1 版本是我实现的 CUDA 上的 baseline 版本,下面对其逻辑稍作解释。
首先,因为串行的 v0 版本中在枚举参考点集所有下标 nInd 时有明显的循环依赖性(当前最优距离依赖于之前的循环迭代结果),因此不可以直接移植到多线程上。为此,我将求解的过程划分成如下两个阶段,从而使每个阶段都没有循环依赖:
- 计算查询点到参考点的距离矩阵
dis,大小为 $m\times n$- 为了减少一次不必要的开方运算,这里保存的是距离的平方
- 对于距离矩阵
dis的每一行,求出其最小值点下标,并保存在答案向量对应位置
为了简化开发过程,在这个 baseline 版本中我使用了 thrust 库进行显存管理,其优点是提供了接近于 STL 的高级抽象,同时又是运行时零开销的。
对于第一阶段计算距离矩阵,我实现了一个核函数 get_dis_kernel,将线程按照 $32\times 32$ 分块并一一映射到距离矩阵的每个位置上。作为 baseline 版本,此处每个线程都直接使用串行逻辑,线程之间没有交互。由于第一阶段程序用时实际上相当小(见下),此处暂且不对 blockDim 的大小进行调整,直接按照经验选择了 1024。
对于第二阶段求距离矩阵最小点,实际上是一个非常经典的区间规约问题,我已经在 CUDA-8 这一节课上学过对应的优化方法。当然,还是有一些小的区别,课件上的规约操作是求和,而我这里是区间最小值点下标。恰好 thrust 库中也有封装好的算法 thrust::min_element ,我这里直接用其作为实现,也可作为后续优化的标杆。
v1 版本中有一个 cudaCallback 函数作为外部调用的接口,还有一个 get_dis_kernel 核函数用于计算上文提到的距离矩阵。
v2
注意到 v1 版本中第二阶段的规约算法占据了九成以上的时间,而且多次使用规约算法时,第二层规约的元素数量会远小于第一层元素的数量,猜测没有充分利用显卡的算力因此效果很差。因此我在 v2 版本中增加了一个核函数 get_min_kernel,按照 CUDA-8 课程的 ppt,使用 share memory 实现了一个 block 内部的树形规约算法。显卡上使用 share memory 进行树形规约的算法已经非常经典,此处不做详细展开了。
调用核函数时,每个 block 内有 1024 个线程(显卡 v100 的上限)按照一维分布;而每个 grid 内有 m 个 block,每个 block 对应一个查询点的求解。程序运行时,每个线程先读入一部分距离向量的元素(此处是跳跃读取,从而使在运行的时候访存连续)并在线程内部进行规约;随后 block 内部的线程使用树形规约求出最小值和对应下标,并保存在 0 号线程中,最后由 0 号线程写回结果。
v2 版本相对于 v1 版本增加了一个 get_min_kernel 核函数,实现了上文提到的树形规约算法。
v3
重新看一下 v2 版本,可以发现这个距离矩阵其实是不必要去计算的,我大可以边计算查询点到参考点的距离边规约求最小值,于是得到了 v3 版本,从而减少了一次启动核函数的开销,和一次对距离矩阵的读写。
v3 版本在启动核函数时,线程在 block 和 grid 中的分布方式与 v2 版本中 get_min_kernel 的方式完全相同。每个线程先串行计算查询点和一部分参考点的距离并规约,随后在 block 内部执行树形规约。
v3 版本中有一个 cudaCallback 函数作为外部调用的接口,还有一个 cudaCallBackKernel 核函数执行上文提到的求距离并执行规约过程。
v4
注意到 TA 提供的接口中,点的存储方式是 Array of Structures(AoS,点的每个维度上的坐标值存储连续),这种存储方式在串行上有空间局部性,比较适合 CPU 的缓存方式,但是在 GPU 上访问的时候却会导致严重的访存不连续问题,且会随着 k 的增加不断的变严重(比如,在 v2 版本中,k 从 3 增加到 16 时,求解距离矩阵的时间从 0.5ms 增加到了 5ms,增加的时间远多于显卡带宽读入对应数据所需的时间)。
我在 v3 版本上额外增加了一个 mat_inv_kernel 核函数,将 TA 提供的参考点坐标进行了一次转置(如果把输入看成一个矩阵的话),从而让点的存储方式变成 Structure of Arrays(SoA,每个维度上点的坐标值存储连续),这样 cudaCallBackKernel 对参考点的访存就连续了。
虽然说矩阵转置的最优实现是使用 shared memory 分块并合并访存,实际上这里不使用 shared memory 运行的时间也只有 0.5ms。并且由于 k 很小(3~16),因此这个矩阵非常「细长」,使用 shared memory 的分块方法未必就有好的效果。
v4 版本中有一个 cudaCallback 函数作为外部调用的接口,一个 cudaCallBackKernel 核函数执行上文提到的求距离并执行规约过程,还有一个 mat_inv_kernel 核函数用于将参考点矩阵进行转置。
v5
v5 版本尝试用 2d texture memory 优化 v3 版本中对参考点的不连续访存,从而避免像 v4 版本中一样做一次额外的矩阵转置。
v5 版本中有一个 cudaCallback 函数作为外部调用的接口,还有一个 cudaCallBackKernel 核函数执行上文提到的求距离并执行规约过程。注意到使用的 v100 显卡计算能力为 7.0 ,对应的 2d texture memory 中矩阵的宽度不能超过 65536,因此 v5 版本仅能处理 $n\le65536$ 大小的输入。如果超过这个限制,v5 版本会直接调用 v4 版本。
v6
v6 版本在 v4 版本上使用 constant memory 优化对查询点的访问。
v6 版本中有一个 cudaCallback 函数作为外部调用的接口,还有一个 cudaCallBackKernel 核函数执行上文提到的求距离并执行规约过程。注意到 const memory 有大小为 64k 的限制,因此 v6 版本仅能处理 $k\times m\le16384$ 大小的输入。如果超过这个限制,v6 版本会直接调用 v4 版本。
v7
注意到 v3~v6 版本都没有处理这个问题:每个查询点仅由一个 block 完成,如果查询点非常少的时候,启动的 block 也非常少,这将导致很多 SM 空置。
v7 版本在 v4 版本的基础上,对每个查询点将有多个 block 进行查询,启动的 block 数量从 cuda 中的 cudaOccupancyMaxActiveBlocksPerMultiprocessor 函数获得,从而保证启动的cudaCallback核函数能够使 SM 满载。(求矩阵转置的核函数跑得很快,没有必要用这个了)
由于多个 block 会求到多个结果,这里多个结果拷贝回 CPU 进行二级规约。由于实际上二级规约的元素非常少,在 CPU 上进行规约的收益高于 GPU。
v7 版本中有一个 cudaCallback 函数作为外部调用的接口,一个 cudaCallBackKernel 核函数执行上文提到的求距离并执行规约过程,还有一个 mat_inv_kernel 核函数用于将参考点矩阵进行转置。
v8
v8 版本在 v7 版本的基础上增加了多卡的实现。具体来说,就是将参考点集均分到每张显卡上,这样每个显卡执行对参考集一个子集的求解,然后在对每张显卡的结果再进行一次规约。
v8 版本中有一个 cudaCallback 函数作为外部调用的接口,一个 cudaCallBackKernel 核函数执行上文提到的求距离并执行规约过程,还有一个 mat_inv_kernel 核函数用于将参考点矩阵进行转置。
v9
v9 版本在 CPU 上构建了一棵 KD-Tree 用于加速最近邻求解。
v9 中有一个 cudaCallback 函数作为外部调用的接口,还有一个 struct KDTreeCPU,其构造函数即为建树过程;还有一个接口 ask ,返回查询点到参考点的最小距离及下标。
v10
v10 版本在 CPU 上构造了一棵 KD-Tree,然后拷贝到 GPU 上,对最近邻的查询在 GPU 上。
v10 中有一个 cudaCallback 函数作为外部调用的接口,还有一个 struct KDTreeGPU,其构造函数即为建树过程;还有一个接口 range_ask ,返回查询点集合到参考点的最小距离及下标。
解释程序中涉及哪些类型的存储器(如,全局内存,共享内存等),并通过分析数据的访存模式及该存储器的特性说明为何使用该种存储器
对于运行在 CPU 上的版本,缓存结构在 C 语言的层面几乎是不可见的,通常来说数据是被存放在内存上,CPU 通过缓存读取;少部分经常访问的数据编译器会将其存放在寄存器中。在 GPU 上的版本,我主要使用了 global memory、shared memory、texture memory、constant memory。
v2~v8 版本中,我在树形规约算法中使用了 shared memory。shared memory 是容量很小,但是低延迟的 on-chip memory,比 global memory 拥有高得多的带宽,可以把它当做可编程的 cache。物理上,每个 SM 包含一个当前正在执行的 block 中所有 thread 共享的低延迟的内存池。shared memory 使得同一个 block 中的 thread 能够相互合作,重用 on-chip 数据,并且能够显著减少 kernel 需要的 global memory 带宽。在本问题中,shared memory 可以被同一个 block 中的线程访问,从而实现线程间的通信,完成多线程并行的的树形规约算法。
v4 版本中,我将 TA 提供的参考点坐标进行了一次转置(如果把输入看成一个矩阵的话),从而让点的存储方式变成 Structure of Arrays(SoA,每个维度上点的坐标值存储连续),这样对 global memory 的访存就连续了。
v5 版本中,我使用 2d texture memory 加速对参考点的访问。texture memory 不需要满足 global memory 的合并访问条件也可以优化邻域上的数据读取。
v6 版本中,我使用 constant memory 加速对查询点的访问。对 constant memory 的单次读操作可以广播到同个半线程束的其他 $15$ 个线程,这种方式产生的内存流量只是使用全局内存时的 $\frac{1}{16}$。同时硬件主动把 constant memory 缓存在 GPU 上,在第一次从常量内存的某个地址上读取后,当其他半线程束请求同一个地址时,那么将命中缓存,这同样减少了额外的内存流量。
针对查询点集为 1 个点及 1024 个点给出两个版本,并说明设计逻辑(例如,任务分配方式)的异同。如两个版本使用同一逻辑,需说明原因
刚看到作业题的时候,我想的是「先实现一个查询点的逻辑,然后扩展到多个点上」。然而实际上在实现的时候,我却先实现了在多个查询点上效果良好而单点效果很差的 v2~v6 版本,然后再增加数据的并行性得到了 v7~v8 版本,优化了其在 1 个查询点上的表现。
原因其实也很明显:多个查询点的版本天生就有很高的并行性,每个查询其实是互不影响的,每个任务分给一个 block 即可,可以同时进行,这样能够充分利用显卡上的大量线程。然而只有一个查询点时,实际上只启动了一个 block,造成了大量计算资源的浪费。
因此,设计的 v7 版本则将之前每个 block 的任务进一步细分,每个 block 只执行原先任务的一个子集;得到的结果经过二次规约之后才是最终的结果。
v8 版本和 v7 版本的任务划分方式完全相同,只不过要先通过多线程划分一次任务,而各线程得到结果在规约时也要设置临界区防止读写冲突。
请给出一个基础版本(baseline)及至少一个优化版本。并分析说明每种优化对性能的影响
我一共实现了 v0~v10 共 11 个版本。由于使用数据结构 KD-Tree 的 v9、v10 版本比较特殊,有一个建树的过程,其 benchmark 方式和其他版本不同,因此对其性能的测试和评价在最后一部分进行(见下文)。
测试方法
测试使用的编译指令如下(打开所有常见编译优化):
1
2
3
set(CMAKE_C_FLAGS "${CMAKE_C_FLAGS} -Ofast -fopenmp")
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -Ofast -fopenmp")
set(CUDA_NVCC_FLAGS "${CUDA_NVCC_FLAGS} -O3 -use_fast_math -Xcompiler -Ofast -Xcompiler -fopenmp")
TA 提供的几组测试数据如下:
| id | k | m | n |
|---|---|---|---|
| 0 | 3 | 1 | 2 |
| 1 | 3 | 2 | 8 |
| 2 | 3 | 1 | 1024 |
| 3 | 3 | 1 | 65536 |
| 4 | 16 | 1 | 65536 |
| 5 | 3 | 1024 | 1024 |
| 6 | 3 | 1024 | 65536 |
| 7 | 16 | 1024 | 65536 |
由于我最后优化的版本在最大的测试数据上已经跑到了 2.689ms,而此时系统噪声对结果的影响已经不能忽视,上述几组数据实际上并不足够反映我优化的效果,我也构造了四组更大的测试:
| id | k | m | n |
|---|---|---|---|
| 8 | 3 | 1 | 16777216 |
| 9 | 16 | 1 | 16777216 |
| 10 | 3 | 1024 | 1048576 |
| 11 | 16 | 1024 | 1048576 |
其中,第 8、9 组数据是对第 3、4 组数据的加强,适用于衡量 1 个参考点集的情况;第 10、11 组数据是对第 6、7 组数据的加强,适用于衡量 1024 个参考点集的情况。我将 benchmark 的过程封装成 class,只需要在 sources/src/core.cu 最后几行中的添加相关内容即可运行。
1
2
3
4
5
6
static WarmUP warm_up(1, 1, 1 << 20);
static BenchMark
benchmark8(3, 1, 1 << 24),
benchmark9(16, 1, 1 << 24),
benchmark10(3, 1024, 1 << 20),
benchmark11(16, 1024, 1 << 20);
此外,实验中发现对于一张显卡上首次运行的核函数会有 30ms 左右的冷启动时间。为排除这部分对于 benchmark 的影响,我也封装了一个 WarmUP class,提前进行「热身」操作。
测试环境
- Intel(R) Xeon(R) Gold 6242 CPU@2.80GHz *2
- 128GB Memory
- NVIDIA(R) Tesla(R) V100 32GB * 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
$ cat /proc/cpuinfo | grep name | cut -f2 -d: | uniq -c
32 Intel(R) Xeon(R) Gold 6242 CPU @ 2.80GHz
$ cat /proc/meminfo | grep Mem
MemTotal: 131660272 kB
MemFree: 97517704 kB
MemAvailable: 126997860 kB
$ nvidia-smi
Sat Jul 18 09:05:07 2020
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 440.33.01 Driver Version: 440.33.01 CUDA Version: 10.2 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla V100-SXM2... Off | 00000000:1A:00.0 Off | 0 |
| N/A 38C P0 41W / 300W | 0MiB / 32510MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 1 Tesla V100-SXM2... Off | 00000000:3D:00.0 Off | 0 |
| N/A 37C P0 42W / 300W | 0MiB / 32510MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 2 Tesla V100-SXM2... Off | 00000000:89:00.0 Off | 0 |
| N/A 37C P0 42W / 300W | 0MiB / 32510MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
| 3 Tesla V100-SXM2... Off | 00000000:B2:00.0 Off | 0 |
| N/A 38C P0 41W / 300W | 0MiB / 32510MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+
测试结果
可以查看当前目录下的 screen.log。
v8(v7)版本对第 0~7 组数据的结果
由于这几组数据都没有让单卡跑满,因此 v8 版本实际上是直接调用 v7 版本实现的,其结果如下(单位为 ms,下同):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 0.929 | 0.620 | 0.600 | 1.832 | 3.294 | 0.403 | 0.925 | 2.689 |
可以看到我的程序跑的还是相当快的。而且运行结果受系统噪声过大,甚至出现了 1 个参考点的数据 4 运行时间比 1024 个参考点的数据 7 还要大的情况,因此此处结果仅供参考,不用于衡量实际测试结果。
v0~v8 版本对第 8~11 组数据的结果
| version | 8 | 9 | 10 | 11 |
|---|---|---|---|---|
| v0 | 46.044 | 201.456 | 2804.439 | 12104.106 |
| v1 | 48.321 | 236.344 | 384.369 | 488.961 |
| v2 | 61.228 | 262.765 | 40.041 | 148.049 |
| v3 | 58.445 | 338.374 | 14.915 | 128.129 |
| v4 | 97.289 | 410.671 | 17.890 | 46.449 |
| v5 | 107.971 | 399.344 | 18.036 | 47.162 |
| v6 | 67.248 | 346.049 | 17.656 | 64.690 |
| v7 | 58.224 | 343.083 | 20.012 | 48.639 |
| v8 | 25.650 | 100.346 | 9.971 | 17.292 |
对上述结果做可视化如下:
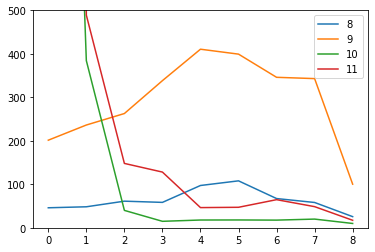
上图中纵轴是程序的运行时间,横轴对应各个版本,不同颜色的折线代表不同数据集的情况。由于 v0 版本是 CPU 上的串行版本,在部分测试数据上运行时间非常久,超过了纵轴的范围,为了图像的直观性其值在图中不显示。
结果分析
从可视化的折线图中可以看出,无论哪一组数据,多卡上的版本都有最优的性能,多卡加速还是非常有效的。下面再对单卡上的 v1~v7 版本进行分析。
首先,对于 1 个查询点的数据来看,直接使用 thrust::min_element 库的 v1 版本就是最优秀的。可以看到,thrust 库能够号称「Code at the speed of light」,还是做了很多优化的。然而,由于这个函数实际上并没有针对多个查询作优化,本身也是线程不安全的(直接 #pragma omp parallel for 会报错),因此其对 1024 个查询点的结果非常不佳。根据测试数据来看,{k, m, n} == {3, 1024, 65536} 时两个阶段所用时间分别为 0.556032ms, 53.586945ms;{k, m, n} == {16, 1024, 65536} 时两个阶段所用时间分别为 5.749760ms, 53.504002ms。这说明九成计算时间都在第二阶段,也为后面的优化方法提供了思路和指导。
直接调库的结果未免有点「胜之不武」,因此在 v2 版本中用我自己的代码代替了 thrust::min_element ,也同时对多个查询进行优化。当然 v2 版本也有一些问题。v2 版本区间规约的核函数只启动了一次,实际上只有一层规约就得到最后结果,而且一个查询点实际上只由一个 block 负责求解,对于 1024 个点的版本来说还好,对于 1 个点的查询实际上只启动了 1 个 block,显然远远不能充分利用显卡的多个 SM!不过相对于 v1 版本,v2 版本中区间规约的时间减少到 3 毫秒以内,相对于 v1 版本已经提高太多了。
v3 版本相当于将 v2 版本中两个核函数融合,因此也继承了 v2 版本的缺点,在查询点只有 1 个的时候实际上只启动了 1 个 block。从运行时间上来看,对于 {k, m, n} == {16, 1024, 65536} 有一定的效果(11ms 减为 9ms),而在输入点只有 1 个的时候时间却增加了非常多(因为求距离时的并行性大大降低了)。
v4 版本相对于 v3 版本,增加的矩阵转置过程本身只用了不到 0.5ms,却让程序在 {k, m, n} == {16, 1024, 65536} 的总运行时间从 9ms 下降到 4ms,效果非常明显!然而,由于每个 block 对只对应一个查询点,因此没有办法通过同样的方法调整查询点的访存。
由于 v5 版本中使用了 texture memory,所以上面第 8~11 组数据上的结果实际上是调用 v4 版本实现的。而从 {k, m, n} == {16, 1024, 65536} 这组测试数据来看,v5 版本的运行时间大概在 6ms 左右,相对于 v3 版本有提升但是不如 v4 版本好。这说明纹理内存的访问速度还是比不上合并访存之后的 global memory。
v6 版本在 v4 版本的基础上使用 constant memory 优化了对查询点的访问,在 v4 版本上少许提升了性能。然而 v6 版本也有缺陷:constant memory 有 64K 的限制,因此只能处理 $k\times m\le 16384$ 的输入。因此后续优化仍然是在 v4 版本上做的。
v7 版本在 v4 版本上增加了算法的并行性,对 SM 的利用率更高,因此同样在 v4 版本的基础上提升了性能表现,同时效果优于 v6。
选做:使用空间划分数据结构加速查询(如 KD-Tree, BVH-Tree)
我实现了使用 CPU 上的 KD-Tree 的 v9 版本、使用 GPU 上的 KD-Tree 的 v10 版本。
KD-Tree 是每个节点都为 k 维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分割成两个半空间。节点左边的子树代表在超平面左边的点,节点右边的子树代表在超平面右边的点。最邻近搜索用来找出在树中与输入点最接近的点,在 KD 树上最邻近搜索的过程如下:
- 从根节点开始,递归的往下移。往左还是往右的决定方法与插入元素的方法一样(如果输入点在分区面的左边则进入左子节点,在右边则进入右子节点)。
- 一旦移动到叶节点,将该节点当「当前最佳点」。
- 解开递归,并对每个经过的节点运行下列步骤:
- 如果当前所在点比当前最佳点更靠近输入点,则将其变为当前最佳点。
- 检查另一边子树有没有更近的点,如果有则从该节点往下找。
- 当根节点搜索完毕后完成最邻近搜索。
首先我实现了纯 CPU 上的 v9 版本,此版本用于检验算法的正确性,且通过了在线评测网站的测试。这个版本中建树有一些小技巧:树的根节点是 1 号点,而节点 i 的左孩子节点是 i << 1,右孩子 i << 1 | 1,这样直接用数学公式就可以推出每个孩子的编号,减少了寻址过程,而空间也没有浪费特别多(对于 n 个参考点的集合,树上顶点编号不超过 $n\times 4$)。此外,在建树时我选择方差最大的维度作为分割,并选择这一维的中位数作为分割点,这样生成的 KD 树是平衡的,每个叶节点的高度都十分接近,并且将空间切割更均匀,在查找时更容易被剪枝。
然后我实现了 GPU 上的 v10 版本。此版本使用 GPU 的多线程加速查找过程,每个线程对应一个查询点,使得其可以同时查询原问题中的多个顶点;其他算法与 CPU 上的一致。
由于使用 KD-Tree 会有一个比较耗时的建树过程,在本问题中如果直接同其他版本比较的话其实是不太公正的,应当把建树和查询的过程分开来看。这样评价也有现实意义,例如某 MOBA 游戏中玩家释放的技能自动定位到最近的野怪,此时单次查询时的「延迟感」对游戏体验的影响非常大,此时使用 KD-Tree 可以大大减少这个延迟,而建树的过程可以放在游戏加载的时候,相对不那么重要。此外,对于 KD-Tree 版本的代码,我发现当数据范围过大时,其建树时间会漫长到让人难以接受。由于时间所限,我使用 {k, m, n} == {3, 1024, 65536} 和 {k, m, n} == {16, 1024, 65536} 这两组数据评价最终的效果。
这里同样放出 CPU 上的 v0 版本和 GPU 上的 v7 版本进行对照。
| 版本 | $k=3$ 查询时间 | $k=3$ 总时间 | $k=16$ 查询时间 | $k=16$ 总时间 |
|---|---|---|---|---|
| v0 | 176.126 | 176.126 | 705.098 | 705.098 |
| v7 | 0.925 | 0.925 | 2.689 | 2.689 |
| v9 | 1.073 | 19.804 | 2419.928 | 2460.956 |
| v10 | 0.433 | 18.755 | 24.292 | 69.975 |
从结果来看,在维数比较低的时候,创建的 KD 树能够有效减少查询时的时间,然而在高维情况下这个空间划分结构显得花哨且不实用,可以说是「维数灾难」了。在高维空间中,KD 树并不能做很高效的最近邻搜索(难以触发搜索时的剪枝条件),从而使大部分的点都会被查询,最终算法效率也不会比全体查询一遍要好到哪里去。
Related posts