CC BY 4.0 （除特别声明或转载文章外）
如果这篇博客帮助到你，可以请我喝一杯咖啡~
2021-10-08：在[email protected]、[email protected]下重新做了这个实验。
因为超算队的新大三队员正在做 CUDA 矩阵乘法的作业，因此给他们安排了一期关于 CUDA 的内培。重看了一年前我在刚学 CUDA 时候做的实验，有些辣眼睛，那重新做一遍这个实验叭
本文基于 CUDA 实现了稠密矩阵乘法过程 $C\to\alpha AB+\beta C$，并在 $A,B,C\in\reals^{2^{13}\times 2^{13}}$ 大小的测试数据上与 cuBLAS 等常见实现进行性能比较。最终在没有内嵌汇编的情况下达到了 NVIDIA V100 GPU 理论性能的 92.1%（14.46 TFLOPS / 15.7 TFLOPS）。同情况下 cuBLAS 性能为 97.0%（15.23 TFLOPS / 15.7 TFLOPS），CUTLASS 库性能为 92.6%（14.54 TFLOPS / 15.7 TFLOPS）。
参考资料
- Exploring the performance of SGEMM in OpenCL on NVIDIA GPUs
- 非常详细的矩阵乘法调优示例
- 基于 OpenCL 实现
- Alcanderian/CUDA-tutorial/sgemm
- 超算队老学长的矩阵乘法示例
- fynv/optimal_sgemm_cuda_c
- optimize the g_sgemm kernel using CUDA C only
- The aim is to achieve a performance like CUTLASS (without wmma), using a very small amount of code
- CUTLASS
- A collection of CUDA C++ template abstractions for implementing high-performance matrix-multiplication (GEMM) at all levels and scales within CUDA.
- cuBLAS
- Almost the most efficient implementations, uses hand-tuned sass code.
实验环境
实验在广州超算中心 TH-2K 集群的一个 gpu_v100 节点上进行。相关硬件环境为：
- NVLINK 接口的 NVIDIA V100 显卡 x4，单卡拥有：
- 5120 个 CUDA 核心
- 5120 个 FP32 单元
- 2560 个 FP64 单元
- 理论单精度算力 $1530\text{MHz}\times5120\text{FP32 units}\times 2\approx 15.7\text{TFLOPS}$
相关软件环境为：
实验过程
这里我只放出自己优化矩阵乘法过程的示例，相关核函数代码都放在 namespace wuk 中。所有矩阵按照 cuBLAS 的习惯，按照列优先方式存储，即 C[i + j * ldc] 表示 $C$ 第 $i$ 行 $j$ 列的元素；这与 C 语言在 CPU 的默认方式（行优先）恰好相反，相关原因会在下文中解释。当然行优先列优先的表示方式之间可以通过一次矩阵转置来调整，因此在应用于实际问题上的时候其实不是一个很让人困扰的问题。
gemm_32x32_v0
严格意义上来说，我是从 gemm_32x32_v1 版本开始优化的，但是 v0 版本仍然可以作为和 v1 版本的对比存在。在 gemm_32x32_v0 版本中，32x32 代表一个 block 计算答案矩阵 $C$ 中一个 $32\times 32$ 的子矩阵的结果（下同）。
在这个版本中，每个线程负责计算答案矩阵的一个元素，各自需要读取 $A$ 矩阵的一行和 $B$ 矩阵的一列，同一个 block 的线程之间没有发生通信。线程的 x 维度对应 $C$ 的列维度，线程的 y 维度对应 $C$ 的行维度。
这个版本的运行时间为 4687.326172 ms，达到的计算效率为 2.345712e+11 FLOPS，甚至没有发挥到理论算力的 1.5%。
gemm_32x32_v1
v1 版本在 v0 版本的基础上调整了线程到 $C$ 矩阵的映射关系，使得线程的 x 维度对应 $C$ 的行维度，线程的 y 维度对应 $C$ 的列维度。对于已经有过一些 CUDA 经验的同学来说，很容易知道这样做有助于触发 GPU 的合并访存，将连续的对 global memory 的读写操作合并成一次操作。
这个还没有分块的矩阵乘法运行时间为 638.216309 ms，几乎已经达到了 Alcanderian 学长以前给大家内培时分块矩阵的 614.487305 ms。原因在哪里？我翻了一下之前的代码，发现学长的代码为了兼容块大小不是 32 的整数倍的情况下的运算时，是通过读取 $A,B,C$ 矩阵时判断 if (a_ir < M && a_ic < K) 等条件实现的，但是这样做显然会带来大量的分支判断，因为 GPU 的分支预测做的远没有 CPU 好，所以带来严重的性能下降。而我在核函数的开始就判断了这个 block 的计算会不会超过矩阵的边界，如果会超过的话则向前移动 $A,B,C$ 的指针，这样就避免了在循环内部判断越界的问题。
当然这样做也存在问题。首先，核函数不能用于任意维度小于 $32$ 的矩阵乘法；但是此时我们完全可以使用矩阵向量乘甚至 CPU 上的 blas 来代替。此外，这个方法也不能解决 $k\mod 32\neq 0$ 的情况，不过也可以靠额外填充 0 实现（为什么不在 $m,n$ 两个维度上填 $0$ 呢？因为填充 $0$ 代码上的开销明显大于我直接移动指针）。最后，这样做也存在部分位置上的元素被读写两次的问题，因此实际上只能用来做 $\beta=0$ 的示例！
gemm_32x32_v2
这个版本是在我写这篇文章时候偶然得到的。相较于 v1 版本，我仅通过把代码中对 threadIdx.x 的访问提前用变量存起来：idx = threadIdx.x，就使得运行时间缩减到了 462.786011 ms，相较于前一个版本提高了 38.9% 的效率！
起先我以为这样的原因是，threadIdx.x 这个变量不是直接存在寄存器里的，每次在使用的时候都要重新加载进寄存器带来了运行时的开销。但是通过检查生成的 PTX ISA 来看并不是这样，二者均在循环前便加载进了寄存器的。那么让我们结合 PTX ISA 解释一下这个问题。
以下是 gemm_32x32_v2 中核心矩阵乘法过程的 PTX ISA：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
BB8_13:
cvt.s64.s32 %rd52, %r58;
add.s64 %rd53, %rd52, %rd12;
shl.b64 %rd54, %rd53, 2;
add.s64 %rd55, %rd64, %rd54;
ld.global.f32 %f22, [%rd68];
ld.global.f32 %f23, [%rd55];
fma.rn.f32 %f24, %f23, %f22, %f40;
add.s64 %rd56, %rd55, %rd15;
ld.global.f32 %f25, [%rd68+4];
ld.global.f32 %f26, [%rd56];
fma.rn.f32 %f27, %f26, %f25, %f24;
add.s64 %rd57, %rd56, %rd15;
ld.global.f32 %f28, [%rd68+8];
ld.global.f32 %f29, [%rd57];
fma.rn.f32 %f30, %f29, %f28, %f27;
add.s64 %rd58, %rd57, %rd15;
ld.global.f32 %f31, [%rd68+12];
ld.global.f32 %f32, [%rd58];
fma.rn.f32 %f40, %f32, %f31, %f30;
add.s64 %rd68, %rd68, 16;
add.s32 %r58, %r58, %r13;
add.s32 %r57, %r57, 4;
setp.lt.s32 %p8, %r57, %r19;
@%p8 bra BB8_13;
而它在 gemm_32x32_v1 中被展开成了这样：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
BB7_12:
mad.lo.s32 %r49, %r63, %r17, %r6;
cvt.u64.u32 %rd44, %r49;
add.s64 %rd45, %rd44, %rd12;
shl.b64 %rd46, %rd45, 2;
add.s64 %rd47, %rd81, %rd46;
add.s32 %r50, %r13, %r63;
cvt.u64.u32 %rd48, %r50;
add.s64 %rd49, %rd48, %rd13;
shl.b64 %rd50, %rd49, 2;
add.s64 %rd51, %rd83, %rd50;
ld.global.f32 %f22, [%rd51];
ld.global.f32 %f23, [%rd47];
fma.rn.f32 %f24, %f23, %f22, %f40;
add.s32 %r51, %r63, 1;
mad.lo.s32 %r52, %r51, %r17, %r6;
cvt.u64.u32 %rd52, %r52;
add.s64 %rd53, %rd52, %rd12;
shl.b64 %rd54, %rd53, 2;
add.s64 %rd55, %rd81, %rd54;
add.s32 %r53, %r13, %r51;
cvt.u64.u32 %rd56, %r53;
add.s64 %rd57, %rd56, %rd13;
shl.b64 %rd58, %rd57, 2;
add.s64 %rd59, %rd83, %rd58;
ld.global.f32 %f25, [%rd59];
ld.global.f32 %f26, [%rd55];
fma.rn.f32 %f27, %f26, %f25, %f24;
add.s32 %r54, %r63, 2;
mad.lo.s32 %r55, %r54, %r17, %r6;
cvt.u64.u32 %rd60, %r55;
add.s64 %rd61, %rd60, %rd12;
shl.b64 %rd62, %rd61, 2;
add.s64 %rd63, %rd81, %rd62;
add.s32 %r56, %r13, %r54;
cvt.u64.u32 %rd64, %r56;
add.s64 %rd65, %rd64, %rd13;
shl.b64 %rd66, %rd65, 2;
add.s64 %rd67, %rd83, %rd66;
ld.global.f32 %f28, [%rd67];
ld.global.f32 %f29, [%rd63];
fma.rn.f32 %f30, %f29, %f28, %f27;
add.s32 %r57, %r63, 3;
mad.lo.s32 %r58, %r57, %r17, %r6;
cvt.u64.u32 %rd68, %r58;
add.s64 %rd69, %rd68, %rd12;
shl.b64 %rd70, %rd69, 2;
add.s64 %rd71, %rd81, %rd70;
add.s32 %r59, %r13, %r57;
cvt.u64.u32 %rd72, %r59;
add.s64 %rd73, %rd72, %rd13;
shl.b64 %rd74, %rd73, 2;
add.s64 %rd75, %rd83, %rd74;
ld.global.f32 %f31, [%rd75];
ld.global.f32 %f32, [%rd71];
fma.rn.f32 %f40, %f32, %f31, %f30;
add.s32 %r63, %r63, 4;
setp.lt.s32 %p8, %r63, %r16;
@%p8 bra BB7_12;
可以看到，前者由编译器做了大小为 4 的循环展开，后者由编译器做了大小为 5 的循环展开。但即使排除这一点，前者平均 6 条指令中有 1 次 fma （4/24）计算，后者则只有 5/58。因此结论单纯就是，[email protected] 没有为前者生成很好的 ISA ，在 ISA 编译到后端代码的时候也没有很好的优化这一过程。很可惜不能随便升级超算中心节点上安装的 418.67 版本驱动，其最高只支持 [email protected]。因此不能验证最新的 [email protected] 是否解决了这一问题。
此外我也注意到，这个不分块版本的矩阵乘法已经比很多实现比较一般的分块矩阵乘法要快了。原因是 v100 上的显存非常奢侈的使用了 HBM2，相较于网上其他矩阵乘法教程中使用的显卡（大多是 GDDR5 显存）已经强大了不少，一定程度上减小了访存问题对性能的影响程度。
gemm_32x32_v3
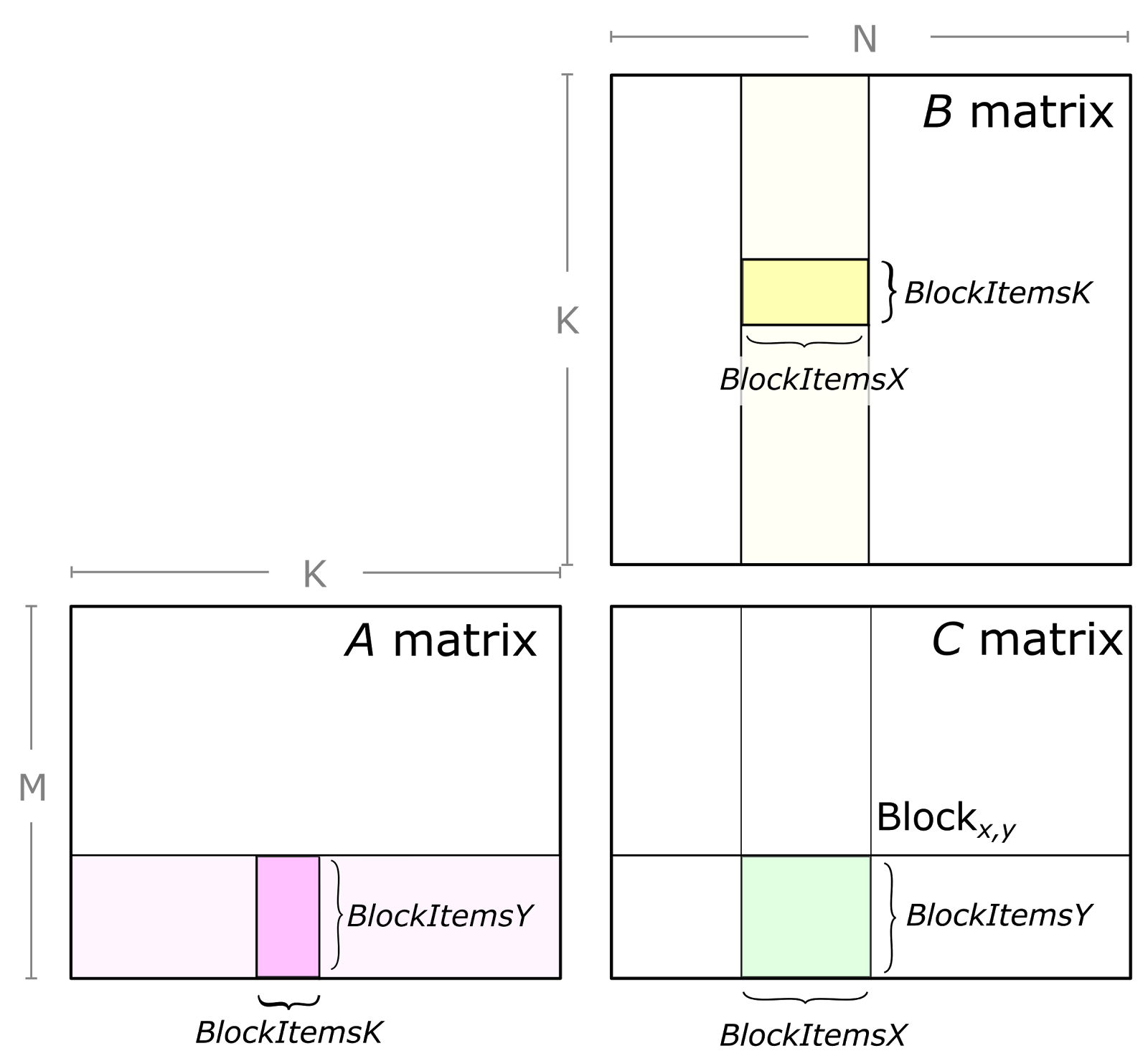
这个版本是最经典的 CUDA 分块矩阵乘法，在互联网上能找到的大部分矩阵乘法实现都是这样做的。
如上图（当然图上为了方便显示只画了 $3\times3$ 分块，实际上是 $32\times 32$ 分块），可以把矩阵分块之后进行计算，这样分过块的子矩阵可以通过读进更快的 shared memory，从而使对 global memoey 的访问流量减少到原先的 $\frac{1}{32}$。随后 block 内的每个线程再分别读子矩阵的一行/一列元素，如下图。
最后运行时间反而退步到了 1565.291992 ms，说明不合理的使用 shared memory 反而会造成严重的性能问题。相较于学长的 cuda_kernel_sgemm_1，提升的地方来自于把矩阵边界的判断从循环内移动到了循环外面。
gemm_32x32_v4
v4 版本在 v3 版本的基础上考虑了 bank conflict 的影响。shared memory 有 32 个 bank，在声明 shared memory 的时候可以通过这样 __shared__ T sA[TILE_WIDTH][TILE_WIDTH | 1]; 的 trick 避免 bank conflict（也可以参照 Alcanderian 学长的 cuda_kernel_sgemm_2 和 cuda_kernel_sgemm_3）。
最后的运行时间为 326.478821 ms，应该是这个经典分块算法能够达到的一个比较好的效果了，但是有效算力只达到了理论算力的 21.7%（3.37 TFLOPS/15.7 FLOPS）。这是由两个原因导致的。一方面，分块矩阵乘法占用了大量的 shared memory，这会限制 block 中活跃线程的数量；另一方面，在编译出来的 PTX ISA 代码中（见下）也可以看到，平均每个有效的 fma 指令要伴随两条对 shared memory 的取指令 ld.shared，那么无形中就浪费了 $\frac{2}{3}$ 的指令吞吐。
1
2
3
ld.shared.f32 %f10, [%r9];
ld.shared.f32 %f11, [%r8];
fma.rn.f32 %f12, %f11, %f10, %f109;
gemm_32x32_v5
v5 版本致力于改善 v4 版本的两条问题，原理基于 PTX ISA 文档中的以下内容：
Limited-length vector types are supported. Vectors of length 2 and 4 of any non-predicate fundamental type can be declared by prefixing the type with .v2 or .v4. Vectors must be based on a fundamental type, and they may reside in the register space. Vectors cannot exceed 128-bits in length; for example, .v4.f64 is not allowed. Three-element vectors may be handled by using a .v4 vector, where the fourth element provides padding. This is a common case for three-dimensional grids, textures, etc.
如上可以发现，显卡支持单线程对不超过 128-bits 的向量类型进行加速操作，那么我们就可以使用内置的 float4 或者 double2 类型来加速访存过程。访存过程主要有四个：对 global memory 的读操作 ld.global、对 global memory 的写操作 st.global 、对 shared memory 的读操作 ld.shared、对 shared memory 的写操作 st.shared。通过向量化加速，我们最多可以同时完成四个 float 元素的访存操作，那我们让一个线程完成原先行维度上四个相邻线程的计算任务即可，如下图（图上是三个线程）。
这个版本的运行时间达到了 203.944931 ms，相对于前一个版本提高了 37%，效果还是非常明显的！检查编译出来的 PTX ISA，可以发现其中确实使用了向量化指令（如 ld.shared.v4.f32），同时核心计算区域里每条有效指令 fma 占的比重已经达到了 $\frac{2}{3}$。
1
2
3
4
5
6
ld.shared.v4.f32 {%f68, %f69, %f70, %f71}, [%r58+128];
ld.shared.f32 %f76, [%r60+4224];
fma.rn.f32 %f77, %f76, %f68, %f64;
fma.rn.f32 %f78, %f76, %f69, %f65;
fma.rn.f32 %f79, %f76, %f70, %f66;
fma.rn.f32 %f80, %f76, %f71, %f67;
此外还有两个值得注意的小细节：
s_B是行优先的方式存储的，这是为了访问 global memory 的过程可以使用ld.global.v4.f32加速，而访问 shared memory 的过程因为开销比较小被战略性放弃了，只能使用单个ld.shared.f32实现（因为物理存储上不连续）。-
如下，在这段代码中我将下次要读取的内容先预加载进寄存器，然后再进行矩阵乘法运算。如果我们把这段代码移动到矩阵乘法之后再进行的话也完全没有问题，但是会导致性能上的明显下降。这是因为单次访存代码的时间很长，很容易导致指令的流水线阻塞。
1 2 3 4 5 6 7
if (l + 32 < k) { A += lda << 5; B += 32; resA = *(Tv *)&A[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * lda]; resB = *(Tv *)&B[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * ldb]; }
gemm_64x64
v5 版本在 v4 版本上优化了有效指令吞吐量到 $\frac{2}{3}$，但是这仍然不是很让人满意的水平；同时对于 s_B 的访问也没有用到向量化加速，让强迫症的我略有不爽；于是考虑一个线程完成一个 $4\times 4$ 小矩阵的计算。当然此时如果一个 block 只计算一个 $32\times 32$ 的子矩阵，那么一个 block 只需要启动 $64$ 个线程，会产生很大的浪费。于是我们让一个 block 对应到原先四个 block 的工作量，即 $64\times 64$，这样仍然需要 256 个线程完成块内计算。
值得注意的是，shared memory 使用的大小是有限制的。我使用的 V100 显卡有着 7.0 的 Compute Capability，单个 block 至多可以使用 96KB 的 shared memory，但是超过 48 KB 的大小只能在运行时动态分配。shared memory 实际上就是可编程的 L1 Cache，其大小可以通过 cudaDeviceSetCacheConfig 调整；shared memory 过大的时候可用的 L1 Cache 就变少了，同样会影响性能。因此，为了方便和其它版本代码进行比较，此处我暂不使用更大的 shared memory，仍然只用 2048 个 float，需要 8KB。这意味着我们需要再次调整对 $A,B$ 矩阵的分块策略，每次读入一个 $64\times 16$ 的 $A$ 矩阵、$16\times 64$ 的 $B$ 矩阵。
分析一下此时的 SM 占有情况：每个 SM 有 96KB 的 shared memory，而每个 block 使用了 8KB，于是每个 SM 中最多分到 12 个 block；12 个 block 一共 3072 线程，大于每个 SM 的最大驻留线程数 2048，因此 SM 占有率是满的。
最终运行时间达到了 83.388191 ms，达到了理论算力的 84%，效果非常显著！再检查一下生成的 PTX ISA 文件，可以发现有效指令吞吐量已经达到了 $\frac{8}{9}$，也符合预期！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ld.shared.v4.f32 {%f147, %f148, %f149, %f150}, [%r79];
ld.shared.v4.f32 {%f155, %f156, %f157, %f158}, [%r80+4096];
fma.rn.f32 %f163, %f147, %f155, %f294;
fma.rn.f32 %f164, %f147, %f156, %f293;
fma.rn.f32 %f165, %f147, %f157, %f292;
fma.rn.f32 %f166, %f147, %f158, %f291;
fma.rn.f32 %f167, %f148, %f155, %f295;
fma.rn.f32 %f168, %f148, %f156, %f296;
fma.rn.f32 %f169, %f148, %f157, %f297;
fma.rn.f32 %f170, %f148, %f158, %f298;
fma.rn.f32 %f171, %f149, %f155, %f299;
fma.rn.f32 %f172, %f149, %f156, %f300;
fma.rn.f32 %f173, %f149, %f157, %f301;
fma.rn.f32 %f174, %f149, %f158, %f302;
fma.rn.f32 %f175, %f150, %f155, %f303;
fma.rn.f32 %f176, %f150, %f156, %f304;
fma.rn.f32 %f177, %f150, %f157, %f305;
fma.rn.f32 %f178, %f150, %f158, %f306;
gemm_128x128
本来我的优化已经到头了，但是又看到了来自 fynv/optimal_sgemm_cuda_c 的代码。原作者水平很高，但是可以看出他也是按照这个顺序去优化的。他是在 $64\times 64$ 的基础上，继续让每个 block 做四个 block 的任务，暴力实现了一个 128x128 的 kernel。此外还做了一些别的 trick，例如使用了两个 Buffer 来回切换，从而省掉一次 __syncthreads()。
那么真的没有继续提升的空间了吗？为了在内培上保住面子，我决定在此基础上再挤出一点点水来。从生成的 PTX ISA 来看，这个循环 for (int j = 0; j < 8; ++j) 并没有被完全展开。于是考虑使用 #pragma unroll(4) 对其进行展开。值得注意的是，在 #pragma unroll(8) 时反而带来了性能下降，猜测是因为代码段太长导致了 Cache Miss。
最终运行时间达到了 76.045088 ms，达到了理论算力的 92.1%。再检查一下生成的 PTX ISA 文件，可以发现有效指令吞吐量已经达到了 $\frac{16}{17}$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
ld.shared.v4.f32 {%f531, %f532, %f533, %f534}, [%r63+512];
ld.shared.v4.f32 {%f539, %f540, %f541, %f542}, [%r63+768];
ld.shared.v4.f32 {%f547, %f548, %f549, %f550}, [%r65+4608];
ld.shared.v4.f32 {%f555, %f556, %f557, %f558}, [%r65+4864];
fma.rn.f32 %f563, %f531, %f547, %f467;
fma.rn.f32 %f564, %f532, %f547, %f468;
fma.rn.f32 %f565, %f533, %f547, %f469;
fma.rn.f32 %f566, %f534, %f547, %f470;
fma.rn.f32 %f567, %f531, %f548, %f471;
fma.rn.f32 %f568, %f532, %f548, %f472;
fma.rn.f32 %f569, %f533, %f548, %f473;
fma.rn.f32 %f570, %f534, %f548, %f474;
fma.rn.f32 %f571, %f531, %f549, %f475;
fma.rn.f32 %f572, %f532, %f549, %f476;
fma.rn.f32 %f573, %f533, %f549, %f477;
fma.rn.f32 %f574, %f534, %f549, %f478;
fma.rn.f32 %f575, %f531, %f550, %f479;
fma.rn.f32 %f576, %f532, %f550, %f480;
fma.rn.f32 %f577, %f533, %f550, %f481;
fma.rn.f32 %f578, %f534, %f550, %f482;
fma.rn.f32 %f579, %f531, %f555, %f483;
fma.rn.f32 %f580, %f532, %f555, %f484;
fma.rn.f32 %f581, %f533, %f555, %f485;
fma.rn.f32 %f582, %f534, %f555, %f486;
fma.rn.f32 %f583, %f531, %f556, %f487;
fma.rn.f32 %f584, %f532, %f556, %f488;
fma.rn.f32 %f585, %f533, %f556, %f489;
fma.rn.f32 %f586, %f534, %f556, %f490;
fma.rn.f32 %f587, %f531, %f557, %f491;
fma.rn.f32 %f588, %f532, %f557, %f492;
fma.rn.f32 %f589, %f533, %f557, %f493;
fma.rn.f32 %f590, %f534, %f557, %f494;
fma.rn.f32 %f591, %f531, %f558, %f495;
fma.rn.f32 %f592, %f532, %f558, %f496;
fma.rn.f32 %f593, %f533, %f558, %f497;
fma.rn.f32 %f594, %f534, %f558, %f498;
fma.rn.f32 %f595, %f539, %f547, %f499;
fma.rn.f32 %f596, %f540, %f547, %f500;
fma.rn.f32 %f597, %f541, %f547, %f501;
fma.rn.f32 %f598, %f542, %f547, %f502;
fma.rn.f32 %f599, %f539, %f548, %f503;
fma.rn.f32 %f600, %f540, %f548, %f504;
fma.rn.f32 %f601, %f541, %f548, %f505;
fma.rn.f32 %f602, %f542, %f548, %f506;
fma.rn.f32 %f603, %f539, %f549, %f507;
fma.rn.f32 %f604, %f540, %f549, %f508;
fma.rn.f32 %f605, %f541, %f549, %f509;
fma.rn.f32 %f606, %f542, %f549, %f510;
fma.rn.f32 %f607, %f539, %f550, %f511;
fma.rn.f32 %f608, %f540, %f550, %f512;
fma.rn.f32 %f609, %f541, %f550, %f513;
fma.rn.f32 %f610, %f542, %f550, %f514;
fma.rn.f32 %f611, %f539, %f555, %f515;
fma.rn.f32 %f612, %f540, %f555, %f516;
fma.rn.f32 %f613, %f541, %f555, %f517;
fma.rn.f32 %f614, %f542, %f555, %f518;
fma.rn.f32 %f615, %f539, %f556, %f519;
fma.rn.f32 %f616, %f540, %f556, %f520;
fma.rn.f32 %f617, %f541, %f556, %f521;
fma.rn.f32 %f618, %f542, %f556, %f522;
fma.rn.f32 %f619, %f539, %f557, %f523;
fma.rn.f32 %f620, %f540, %f557, %f524;
fma.rn.f32 %f621, %f541, %f557, %f525;
fma.rn.f32 %f622, %f542, %f557, %f526;
fma.rn.f32 %f623, %f539, %f558, %f527;
fma.rn.f32 %f624, %f540, %f558, %f528;
fma.rn.f32 %f625, %f541, %f558, %f529;
fma.rn.f32 %f626, %f542, %f558, %f530;
总结
可以发现，越是优化到后面，代码中 for 循环的层级就越多，这与 CUTLASS 库的实现理念 非常接近。究其原因，还是因为 CUDA 在设计上存在明显的层次性结构。如下图，当然我们这里并没有用到 warp-level GEMM，因为 wmma 指令只能作用于半精度矩阵乘法。
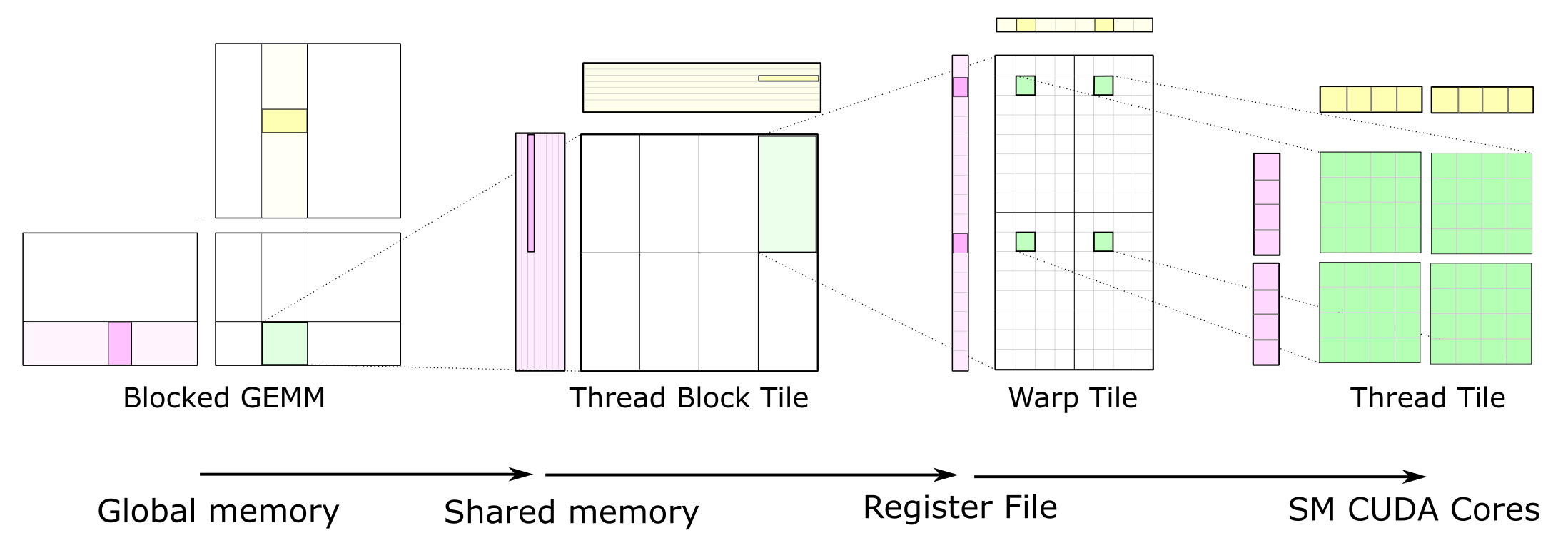
那么最后，矩阵乘法做到这里是不是就到头了呢？我觉得未必。例如，单个 block 至多可以使用 96KB 的 shared memory，单个 thread 至多可以使用 255 个 32-bit 寄存器（256 线程下，因为每个 block 只能有 64K 寄存器），因此我觉得还可以通过增大分块大小继续压榨显卡的性能，而且还可以考虑非正方形分块、分块边长不是 2 的整数幂的情况；再比如某些时候的通信可以直接通过 warp shuffle 指令完成，不需要通过 shared memory；最后，如果认真读过上面所有优化过程的同学可以发现，如果对 B 矩阵提前做一个转置，同样可以使性能获得略微提升（因为此时 s_B 不需要转置存放了）。再进一步就不可避免的要进入汇编优化代码的领域了，我们需要：调整每条指令的顺序以获得最大的有效指令吞吐；调整寄存器的映射，最小化寄存器的 bank conflict（不错，寄存器也是有 bank 的！）；调度好每个寄存器资源，避免不必要的浪费，从而获得更大的分块。
此外 v2 版本被发现的过程也说明 CUDA 的编译器确实没有那么智能，甚至可以说一份高性能的 CUDA 代码可能第一眼让人读上去感觉非常丑。CUDA 虽然目前已被市场证明是比较成功的 GPGPU 编程语言（甚至其老对手 AMD 也几乎抛弃了半死不活的 OpenCL，推出了镜像级复刻的 ROCm 和 HIP，甚至有一个一键转换的 CUDA to HIP 脚本），但是给我的感觉还是设计的上手门槛高了一些，想写出高性能的 CUDA 代码并不能像写 CPU 上的 C 语言一样随心所欲，而需要了解更多硬件上的设计细节。当然了，虽然号称代码里没有使用汇编，但是要想说明优化的效果还是应该结合 PTX ISA 甚至更进一步的 SASS 汇编。
想来半年前在做先导杯的时候只实现到 v5 版本的矩阵乘法就放弃了，半年后自己终于有空完整梳理一遍，写到这里让我觉得已经学到了很多东西。那就完结撒花叭~
源代码
slurm-696755.out
实验的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 460.73.01 Driver Version: 460.73.01 CUDA Version: 11.2 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|===============================+======================+======================|
| 0 Tesla V100-SXM2... Off | 00000000:8A:00.0 Off | 0 |
| N/A 37C P0 38W / 300W | 0MiB / 16160MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
| 1 Tesla V100-SXM2... Off | 00000000:8B:00.0 Off | 0 |
| N/A 32C P0 38W / 300W | 0MiB / 16160MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
| 2 Tesla V100-SXM2... Off | 00000000:B3:00.0 Off | 0 |
| N/A 32C P0 38W / 300W | 0MiB / 16160MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
| 3 Tesla V100-SXM2... Off | 00000000:B4:00.0 Off | 0 |
| N/A 34C P0 38W / 300W | 0MiB / 16160MiB | 0% Default |
| | | N/A |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: |
| GPU GI CI PID Type Process name GPU Memory |
| ID ID Usage |
|=============================================================================|
| No running processes found |
+-----------------------------------------------------------------------------+
clocks.max.sm [MHz]
1530 MHz
cublasSgemm: 71.745537 ms, 1.532516e+13 FLOPS.
CutlassSgemmNN: 79.368195 ms, 1.385330e+13 FLOPS.
Alcanderian::cuda_kernel_sgemm_1: 2114.584473 ms, 5.199658e+11 FLOPS.
Alcanderian::cuda_kernel_sgemm_2: 611.853333 ms, 1.797018e+12 FLOPS.
Alcanderian::cuda_kernel_sgemm_3: 2115.368896 ms, 5.197730e+11 FLOPS.
fynv::g_fgemm: 77.543427 ms, 1.417930e+13 FLOPS.
wuk::gemm_32x32_v0: 4670.738281 ms, 2.354042e+11 FLOPS.
wuk::gemm_32x32_v1: 512.018433 ms, 2.147406e+12 FLOPS.
wuk::gemm_32x32_v2: 458.981384 ms, 2.395547e+12 FLOPS.
wuk::gemm_32x32_v3: 1565.510620 ms, 7.023342e+11 FLOPS.
wuk::gemm_32x32_v4: 324.259827 ms, 3.390835e+12 FLOPS.
wuk::gemm_32x32_v5: 203.590652 ms, 5.400600e+12 FLOPS.
wuk::gemm_64x64: 80.806915 ms, 1.360665e+13 FLOPS.
wuk::gemm_128x128: 76.198914 ms, 1.442949e+13 FLOPS.
gemm.th2k.slurm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#!/bin/bash
#SBATCH -J WuK
#SBATCH -p gpu_v100
#SBATCH -N 1
#SBATCH --exclusive
DIR=/GPUFS/sysu_hpcedu_302/WuK
cd $DIR
if [[ ! -f cutlass-2.7.0.zip ]]; then
curl -o cutlass-2.7.0.zip https://github.com/NVIDIA/cutlass/archive/v2.7.0.zip
unzip cutlass-2.7.0.zip
fi
module purge
module load gcc/6.5.0
module load CUDA/11.2
nvidia-smi
nvidia-smi --query-gpu=clocks.max.sm --format=csv --id=0
nvcc -arch=sm_70 -Icutlass-2.7.0/include -Icutlass-2.7.0/tools/util/include -ptx -o gemm.ptx gemm.cu
nvcc -arch=sm_70 -Icutlass-2.7.0/include -Icutlass-2.7.0/tools/util/include -lcublas -run -o gemm gemm.cu
gemm.cu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
966
#include <cstdio>
#include <cublas_v2.h>
#include <cuda_runtime.h>
#include <cutlass/gemm/device/gemm.h>
#include <cutlass/util/host_tensor.h>
#include <cutlass/util/reference/device/tensor_fill.h>
#include <functional>
///////////////////////////////////////////////////////////////////////////////////////////////////
//
// This function defines a CUTLASS GEMM kernel instantiation, constructs its
// parameters object, and launches it on the CUDA device.
//
///////////////////////////////////////////////////////////////////////////////////////////////////
/// Define a CUTLASS GEMM template and launch a GEMM kernel.
cudaError_t CutlassSgemmNN(int M, int N, int K, float alpha, float const *A,
int lda, float const *B, int ldb, float beta,
float *C, int ldc) {
// Define type definition for single-precision CUTLASS GEMM with column-major
// input matrices and 128x128x8 threadblock tile size (chosen by default).
//
// To keep the interface manageable, several helpers are defined for plausible
// compositions including the following example for single-precision GEMM.
// Typical values are used as default template arguments. See
// `cutlass/gemm/device/default_gemm_configuration.h` for more details.
//
// To view the full gemm device API interface, see
// `cutlass/gemm/device/gemm.h`
using ColumnMajor = cutlass::layout::ColumnMajor;
using CutlassGemm =
cutlass::gemm::device::Gemm<float, // Data-type of A matrix
ColumnMajor, // Layout of A matrix
float, // Data-type of B matrix
ColumnMajor, // Layout of B matrix
float, // Data-type of C matrix
ColumnMajor>; // Layout of C matrix
// Define a CUTLASS GEMM type
CutlassGemm gemm_operator;
// Construct the CUTLASS GEMM arguments object.
//
// One of CUTLASS's design patterns is to define gemm argument objects that
// are constructible in host code and passed to kernels by value. These may
// include pointers, strides, scalars, and other arguments needed by Gemm and
// its components.
//
// The benefits of this pattern are (1.) a structured, composable strategy for
// passing host-constructible arguments to kernels and (2.) minimized
// initialization overhead on kernel entry.
//
CutlassGemm::Arguments args(
{M, N, K}, // Gemm Problem dimensions
{A, lda}, // Tensor-ref for source matrix A
{B, ldb}, // Tensor-ref for source matrix B
{C, ldc}, // Tensor-ref for source matrix C
{C, ldc}, // Tensor-ref for destination matrix D (may be different memory
// than source C matrix)
{alpha, beta}); // Scalars used in the Epilogue
//
// Launch the CUTLASS GEMM kernel.
//
cutlass::Status status = gemm_operator(args);
//
// Return a cudaError_t if the CUTLASS GEMM operator returned an error code.
//
if (status != cutlass::Status::kSuccess) {
return cudaErrorUnknown;
}
// Return success, if no errors were encountered.
return cudaSuccess;
}
namespace Alcanderian // https://github.com/Alcanderian/CUDA-tutorial/sgemm
{
__global__ void cuda_kernel_sgemm_1(float *a, float *b, float *c, size_t N,
size_t M, size_t K, float alpha,
float beta) {
int tr = threadIdx.x; // row idx in block
int tc = threadIdx.y; // col idx in block
int ir = blockIdx.x * 32 + threadIdx.x; // row idx in global
int ic = blockIdx.y * 32 + threadIdx.y; // col idx in global
__shared__ float a_sub[32][32];
__shared__ float b_sub[32][32];
int load_size = K / 32;
if (K % 32 != 0) {
load_size += 1;
}
float acc = 0.0f;
int a_ir = ir;
int b_ic = ic;
#define idx(ri, ci, nc) ((ri) * (nc) + (ci))
for (int l = 0; l < load_size; ++l) {
int a_ic = l * 32 + tc;
int b_ir = l * 32 + tr;
a_sub[tr][tc] = 0.0f;
b_sub[tr][tc] = 0.0f;
if (a_ir < M && a_ic < K)
a_sub[tr][tc] = a[idx(a_ir, a_ic, K)];
if (b_ir < K && b_ic < N)
b_sub[tr][tc] = b[idx(b_ir, b_ic, N)];
__syncthreads();
#pragma unroll
for (int k = 0; k < 32; ++k) {
acc += a_sub[tr][k] * b_sub[k][tc];
}
__syncthreads();
}
if (ir < M && ic < N)
c[idx(ir, ic, N)] = alpha * acc + beta * c[idx(ir, ic, N)];
#undef idx
}
// use __ldg & avoid bank conflict
__global__ void cuda_kernel_sgemm_2(float *__restrict__ a,
float *__restrict__ b,
float *__restrict__ c, size_t N, size_t M,
size_t K, float alpha, float beta) {
int tr = threadIdx.x; // row idx in block
int tc = threadIdx.y; // col idx in block
int ir = blockIdx.x * 32 + threadIdx.x; // row idx in global
int ic = blockIdx.y * 32 + threadIdx.y; // col idx in global
__shared__ float a_sub[32][32 + 1]; // avoid bank conflict
__shared__ float b_sub[32][32 + 1];
int load_size = K / 32;
if (K % 32 != 0) {
load_size += 1;
}
float acc = 0.0f;
int a_ir = ir;
int b_ic = ic;
#define idx(ri, ci, nc) ((ri) * (nc) + (ci))
for (int l = 0; l < load_size; ++l) {
int a_ic = l * 32 + tc;
int b_ir = l * 32 + tr;
a_sub[tr][tc] = 0.0f;
b_sub[tr][tc] = 0.0f;
if (a_ir < M && a_ic < K)
a_sub[tr][tc] = a[idx(a_ir, a_ic, K)];
if (b_ir < K && b_ic < N)
b_sub[tr][tc] = b[idx(b_ir, b_ic, N)];
__syncthreads();
#pragma unroll
for (int k = 0; k < 32; ++k) {
acc += a_sub[tr][k] * b_sub[k][tc];
}
__syncthreads();
}
if (ir < M && ic < N)
c[idx(ir, ic, N)] = alpha * acc + beta * c[idx(ir, ic, N)];
#undef idx
}
// use __ldg without avoiding bank conflict
__global__ void cuda_kernel_sgemm_3(float *__restrict__ a,
float *__restrict__ b,
float *__restrict__ c, size_t N, size_t M,
size_t K, float alpha, float beta) {
int tr = threadIdx.x; // row idx in block
int tc = threadIdx.y; // col idx in block
int ir = blockIdx.x * 32 + threadIdx.x; // row idx in global
int ic = blockIdx.y * 32 + threadIdx.y; // col idx in global
__shared__ float a_sub[32][32]; // avoid bank conflict
__shared__ float b_sub[32][32];
int load_size = K / 32;
if (K % 32 != 0) {
load_size += 1;
}
float acc = 0.0f;
int a_ir = ir;
int b_ic = ic;
#define idx(ri, ci, nc) ((ri) * (nc) + (ci))
for (int l = 0; l < load_size; ++l) {
int a_ic = l * 32 + tc;
int b_ir = l * 32 + tr;
a_sub[tr][tc] = 0.0f;
b_sub[tr][tc] = 0.0f;
if (a_ir < M && a_ic < K)
a_sub[tr][tc] = a[idx(a_ir, a_ic, K)];
if (b_ir < K && b_ic < N)
b_sub[tr][tc] = b[idx(b_ir, b_ic, N)];
__syncthreads();
#pragma unroll
for (int k = 0; k < 32; ++k) {
acc += a_sub[tr][k] * b_sub[k][tc];
}
__syncthreads();
}
if (ir < M && ic < N)
c[idx(ir, ic, N)] = alpha * acc + beta * c[idx(ir, ic, N)];
#undef idx
}
}; // namespace Alcanderian
namespace fynv // https://github.com/fynv/optimal_sgemm_cuda_c
{
struct f8 {
float4 a, b;
__device__ inline f8() { memset(this, 0, sizeof(f8)); }
};
struct f88 {
f8 a, b, c, d, e, f, g, h;
};
__device__ inline void d_load8(const float *p, f8 &c) {
c.a = ((float4 *)p)[0];
c.b = ((float4 *)p)[16];
}
__device__ inline void d_store8(float *p, const f8 &c) {
((float4 *)p)[0] = c.a;
((float4 *)p)[16] = c.b;
}
__device__ inline void d_mult8v(f8 &c, const f8 &a, float b) {
c.a.x += a.a.x * b;
c.a.y += a.a.y * b;
c.a.z += a.a.z * b;
c.a.w += a.a.w * b;
c.b.x += a.b.x * b;
c.b.y += a.b.y * b;
c.b.z += a.b.z * b;
c.b.w += a.b.w * b;
}
template <typename T> __device__ inline void Swap(T &a, T &b) {
T t = a;
a = b;
b = t;
}
__global__ __launch_bounds__(
256) // https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#launch-bounds
void g_fgemm(float *d_C, const float *d_A, const float *d_B, int n, int lda,
int ldb, int ldc) {
int x_a = threadIdx.x & 31;
int y_a = threadIdx.x >> 5;
int x_b = threadIdx.x & 1;
int y_b = threadIdx.x >> 1;
int x_c = threadIdx.x & 15;
int y_c = threadIdx.x >> 4;
__shared__ float smem[4096];
float *s_A1 = smem;
float *s_A2 = smem + 1024;
float *s_B1 = smem + 2048;
float *s_B2 = smem + 3072;
f88 l_C;
const float *p_A = d_A + (blockIdx.x << 7);
const float *p_B = d_B + (blockIdx.y << 7) * ldb;
float4 p, q;
p = ((float4 *)p_A)[y_a * (lda >> 2) + x_a];
q = ((float4 *)p_B)[y_b * (ldb >> 2) + x_b];
for (int i = 0; i < n; i += 8) {
((float4 *)s_A1)[threadIdx.x] = p;
s_B1[(((x_b << 2) + 0) << 7) + y_b] = q.x;
s_B1[(((x_b << 2) + 1) << 7) + y_b] = q.y;
s_B1[(((x_b << 2) + 2) << 7) + y_b] = q.z;
s_B1[(((x_b << 2) + 3) << 7) + y_b] = q.w;
__syncthreads();
if (i + 8 < n) {
p_A += (lda << 3);
p_B += 8;
p = ((float4 *)p_A)[y_a * (lda >> 2) + x_a];
q = ((float4 *)p_B)[y_b * (ldb >> 2) + x_b];
}
for (int j = 0; j < 8; j++) {
float *p_s_A = s_A1 + (j << 7) + (x_c << 2);
float *p_s_B = s_B1 + (j << 7) + (y_c << 2);
f8 a, b;
d_load8(p_s_A, a);
d_load8(p_s_B, b);
d_mult8v(l_C.a, a, b.a.x);
d_mult8v(l_C.b, a, b.a.y);
d_mult8v(l_C.c, a, b.a.z);
d_mult8v(l_C.d, a, b.a.w);
d_mult8v(l_C.e, a, b.b.x);
d_mult8v(l_C.f, a, b.b.y);
d_mult8v(l_C.g, a, b.b.z);
d_mult8v(l_C.h, a, b.b.w);
}
Swap(s_A1, s_A2);
Swap(s_B1, s_B2);
}
float *p_C = d_C + ((blockIdx.x << 7) + (x_c << 2)) +
((blockIdx.y << 7) + (y_c << 2)) * ldc;
d_store8(p_C, l_C.a);
p_C += ldc;
d_store8(p_C, l_C.b);
p_C += ldc;
d_store8(p_C, l_C.c);
p_C += ldc;
d_store8(p_C, l_C.d);
p_C += (ldc * 61);
d_store8(p_C, l_C.e);
p_C += ldc;
d_store8(p_C, l_C.f);
p_C += ldc;
d_store8(p_C, l_C.g);
p_C += ldc;
d_store8(p_C, l_C.h);
}
}; // namespace fynv
namespace wuk {
#define IDX2C(i, j, ld) (((j) * (ld)) + (i))
template <typename T>
__global__
__launch_bounds__(1024) void gemm_32x32_v0(int m, int n, int k, T alpha,
const T *A, int lda, const T *B,
int ldb, T beta, T *C, int ldc) {
const int y_range = ((int)blockIdx.y + 1 << 5) - m,
x_range = ((int)blockIdx.x + 1 << 5) - n;
if (y_range > 0) {
A -= y_range;
C -= y_range;
}
if (x_range > 0) {
B -= x_range * ldb;
C -= x_range * ldc;
}
A += blockIdx.y << 5;
B += (blockIdx.x << 5) * ldb;
C += (blockIdx.y << 5) + (blockIdx.x << 5) * ldc;
T resC = 0;
for (int i = 0; i < k; ++i) {
const T resA = A[IDX2C(threadIdx.y, i, lda)],
resB = B[IDX2C(i, threadIdx.x, ldb)];
resC += resA * resB;
}
resC = resC * alpha + C[IDX2C(threadIdx.y, threadIdx.x, ldc)] * beta;
C[IDX2C(threadIdx.y, threadIdx.x, ldc)] = resC;
}
template <typename T>
__global__
__launch_bounds__(1024) void gemm_32x32_v1(int m, int n, int k, T alpha,
const T *A, int lda, const T *B,
int ldb, T beta, T *C, int ldc) {
const int x_range = ((int)blockIdx.x + 1 << 5) - m,
y_range = ((int)blockIdx.y + 1 << 5) - n;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 5;
B += (blockIdx.y << 5) * ldb;
C += (blockIdx.x << 5) + (blockIdx.y << 5) * ldc;
T resC = 0;
for (int i = 0; i < k; ++i) {
const T resA = A[IDX2C(threadIdx.x, i, lda)],
resB = B[IDX2C(i, threadIdx.y, ldb)];
resC += resA * resB;
}
resC = resC * alpha + C[IDX2C(threadIdx.x, threadIdx.y, ldc)] * beta;
C[IDX2C(threadIdx.x, threadIdx.y, ldc)] = resC;
}
template <typename T>
__global__
__launch_bounds__(1024) void gemm_32x32_v2(int m, int n, int k, T alpha,
const T *A, int lda, const T *B,
int ldb, T beta, T *C, int ldc) {
const int idx = threadIdx.x, idy = threadIdx.y,
x_range = ((int)blockIdx.x + 1 << 5) - m,
y_range = ((int)blockIdx.y + 1 << 5) - n;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 5;
B += (blockIdx.y << 5) * ldb;
C += (blockIdx.x << 5) + (blockIdx.y << 5) * ldc;
T resC = 0;
for (int i = 0; i < k; ++i) {
const T resA = A[IDX2C(idx, i, lda)], resB = B[IDX2C(i, idy, ldb)];
resC += resA * resB;
}
resC = resC * alpha + C[IDX2C(idx, idy, ldc)] * beta;
C[IDX2C(idx, idy, ldc)] = resC;
}
template <typename T, int TILE_WIDTH>
__global__ __launch_bounds__(TILE_WIDTH *TILE_WIDTH) void gemm_32x32_v3(
int m, int n, int k, T alpha, const T *A, int lda, const T *B, int ldb,
T beta, T *C, int ldc) {
const int idx = threadIdx.x, idy = threadIdx.y,
x_range = ((int)blockIdx.x + 1 << 5) - m,
y_range = ((int)blockIdx.y + 1 << 5) - n;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 5;
B += (blockIdx.y << 5) * ldb;
C += (blockIdx.x << 5) + (blockIdx.y << 5) * ldc;
T resC = 0;
__shared__ T sA[TILE_WIDTH][TILE_WIDTH];
__shared__ T sB[TILE_WIDTH][TILE_WIDTH];
for (int i = 0; i < k; i += TILE_WIDTH) {
sA[idx][idy] = A[IDX2C(idx, i + idy, lda)];
sB[idx][idy] = B[IDX2C(i + idx, idy, ldb)];
__syncthreads();
for (int j = 0; j < TILE_WIDTH; ++j)
resC += sA[idx][j] * sB[j][idy];
__syncthreads();
}
resC = resC * alpha + C[IDX2C(idx, idy, ldc)] * beta;
C[IDX2C(idx, idy, ldc)] = resC;
}
template <typename T, int TILE_WIDTH>
__global__ __launch_bounds__(TILE_WIDTH *TILE_WIDTH) void gemm_32x32_v4(
int m, int n, int k, T alpha, const T *A, int lda, const T *B, int ldb,
T beta, T *C, int ldc) {
const int idx = threadIdx.x, idy = threadIdx.y,
x_range = ((int)blockIdx.x + 1 << 5) - m,
y_range = ((int)blockIdx.y + 1 << 5) - n;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 5;
B += (blockIdx.y << 5) * ldb;
C += (blockIdx.x << 5) + (blockIdx.y << 5) * ldc;
T resC = 0;
__shared__ T sA[TILE_WIDTH][TILE_WIDTH | 1];
__shared__ T sB[TILE_WIDTH][TILE_WIDTH | 1];
for (int i = 0; i < k; i += TILE_WIDTH) {
sA[idx][idy] = A[IDX2C(idx, i + idy, lda)];
sB[idx][idy] = B[IDX2C(i + idx, idy, ldb)];
__syncthreads();
for (int j = 0; j < TILE_WIDTH; ++j)
resC += sA[idx][j] * sB[j][idy];
__syncthreads();
}
resC = resC * alpha + C[IDX2C(idx, idy, ldc)] * beta;
C[IDX2C(idx, idy, ldc)] = resC;
}
#undef IDX2C
template <typename T, typename Tv, int TWO_BUFFER>
__global__
__launch_bounds__(256) void gemm_32x32_v5(int m, int n, int k, T alpha,
const T *A, int lda, const T *B,
int ldb, T beta, T *C, int ldc) {
const int TvSize = sizeof(Tv) / sizeof(T), idx = threadIdx.x,
x_range = ((int)blockIdx.x + 1 << 5) - m,
y_range = ((int)blockIdx.y + 1 << 5) - n;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 5;
B += (blockIdx.y << 5) * ldb;
C += (blockIdx.x << 5) + (blockIdx.y << 5) * ldc;
Tv ansC;
memset(&ansC, 0, sizeof(ansC));
__shared__ T s_buffer[2048];
T *s_A = s_buffer;
T *s_B = s_buffer + 1024;
#if TWO_BUFFER
__shared__ T s_tbuffer[2048];
T *s_tA = s_tbuffer;
T *s_tB = s_tbuffer + 1024;
#endif
Tv resA = *(Tv *)&A[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * lda],
resB = *(Tv *)&B[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * ldb];
for (int l = 0; l < k; l += 32) {
((Tv *)s_A)[idx] = resA;
for (int i = 0; i < TvSize; ++i)
s_B[(((idx * TvSize) & 31) << 5) + ((idx * TvSize) >> 5)] =
((T *)&resB)[i];
__syncthreads();
if (l + 32 < k) {
A += lda << 5;
B += 32;
resA = *(Tv *)&A[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * lda];
resB = *(Tv *)&B[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * ldb];
}
for (int j = 0; j < 32; ++j) {
Tv tmpA = *(Tv *)&s_A[((idx * TvSize) & 31) + (j << 5)];
T tmpB = s_B[(j << 5) + ((idx * TvSize) >> 5)];
for (int i = 0; i < TvSize; ++i)
((T *)&ansC)[i] += ((T *)&tmpA)[i] * tmpB;
}
#if TWO_BUFFER
{
T *tmp_A = s_A;
s_A = s_tA;
s_tA = tmp_A;
}
{
T *tmp_B = s_B;
s_B = s_tB;
s_tB = tmp_B;
}
#else
__syncthreads();
#endif
}
{
Tv *devC = (Tv *)&C[((idx * TvSize) & 31) + ((idx * TvSize) >> 5) * ldc],
resC = *devC;
for (int i = 0; i < TvSize; ++i)
((T *)&resC)[i] = alpha * ((T *)&ansC)[i] + beta * ((T *)&resC)[i];
*devC = resC;
}
}
template <typename T, typename Tv, int TWO_BUFFER>
__global__ __launch_bounds__(256) void gemm_64x64(int m, int n, int k, T alpha,
const T *A, int lda,
const T *B, int ldb, T beta,
T *C, int ldc) {
const int TvSize = sizeof(Tv) / sizeof(T), idx = threadIdx.x,
x_range = ((int)blockIdx.x + 1 << 6) - m,
y_range = ((int)blockIdx.y + 1 << 6) - n;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 6;
B += (blockIdx.y << 6) * ldb;
C += (blockIdx.x << 6) + (blockIdx.y << 6) * ldc;
Tv ansC[TvSize];
memset(ansC, 0, sizeof(ansC));
__shared__ T s_buffer[2048];
T *s_A = s_buffer;
T *s_B = s_buffer + 1024;
#if TWO_BUFFER
__shared__ T s_tbuffer[2048];
T *s_tA = s_tbuffer;
T *s_tB = s_tbuffer + 1024;
#endif
Tv resA = *(Tv *)&(A[((idx * TvSize) & 63) + ((idx * TvSize) >> 6) * lda]),
resB = *(Tv *)&(B[((idx * TvSize) & 15) + ((idx * TvSize) >> 4) * ldb]);
for (int l = 0; l < k; l += 16) {
((Tv *)s_A)[idx] = resA;
for (int i = 0; i < TvSize; ++i)
s_B[((((idx * TvSize) & 15) + i) << 6) + ((idx * TvSize) >> 4)] =
((T *)&resB)[i];
__syncthreads();
if (l + 16 < k) {
A += lda << 4;
B += 16;
resA = *(Tv *)&(A[((idx * TvSize) & 63) + ((idx * TvSize) >> 6) * lda]);
resB = *(Tv *)&(B[((idx * TvSize) & 15) + ((idx * TvSize) >> 4) * ldb]);
}
for (int j = 0; j < 16; ++j) {
const Tv tmpA = *(Tv *)&(s_A[((idx * TvSize) & 63) + (j << 6)]),
tmpB = *(Tv *)&(s_B[(j << 6) + (idx >> 4) * TvSize]);
for (int i = 0; i < TvSize; ++i)
for (int h = 0; h < TvSize; ++h)
((T *)&ansC[i])[h] += ((T *)&tmpA)[i] * ((T *)&tmpB)[h];
}
#if TWO_BUFFER
{
T *tmp_A = s_A;
s_A = s_tA;
s_tA = tmp_A;
}
{
T *tmp_B = s_B;
s_B = s_tB;
s_tB = tmp_B;
}
#else
__syncthreads();
#endif
}
for (int i = 0; i < TvSize; ++i) {
Tv *devC = (Tv *)&(C[(idx & 15) * 4 + ((idx >> 4) * 4 + i) * ldc]),
resC = *devC;
for (int h = 0; h < TvSize; ++h)
((T *)&resC)[h] = alpha * ((T *)&ansC[i])[h] + beta * ((T *)&resC)[h];
*devC = resC;
}
}
template <typename T, typename Tv, int TWO_BUFFER>
__global__
__launch_bounds__(256) void gemm_128x128(int m, int n, int k, T alpha,
const T *A, int lda, const T *B,
int ldb, T beta, T *C, int ldc) {
const int TvSize = sizeof(Tv) / sizeof(T), idx = threadIdx.x,
x_range = ((int)blockIdx.x + 1 << 7) - m,
y_range = ((int)blockIdx.y + 1 << 7) - n, x_a = idx & 31,
y_a = idx >> 5, x_b = idx & 1, y_b = idx >> 1, x_c = idx & 15,
y_c = idx >> 4;
if (x_range > 0) {
A -= x_range;
C -= x_range;
}
if (y_range > 0) {
B -= y_range * ldb;
C -= y_range * ldc;
}
A += blockIdx.x << 7;
B += (blockIdx.y << 7) * ldb;
C +=
((blockIdx.x << 7) + (x_c << 2)) + ((blockIdx.y << 7) + (y_c << 2)) * ldc;
__shared__ T s_buffer[2048];
T *s_A = s_buffer;
T *s_B = s_buffer + 1024;
#if TWO_BUFFER
__shared__ T s_tbuffer[2048];
T *s_tA = s_tbuffer;
T *s_tB = s_tbuffer + 1024;
#endif
Tv ansC[2][2][TvSize];
memset(ansC, 0, sizeof(ansC));
Tv resA = ((Tv *)A)[x_a + y_a * (lda >> 2)];
Tv resB = ((Tv *)B)[x_b + y_b * (ldb >> 2)];
for (int l = 0; l < k; l += 8) {
((Tv *)s_A)[idx] = resA;
for (int i = 0; i < TvSize; ++i)
s_B[(((x_b << 2) + i) << 7) + y_b] = ((T *)&resB)[i];
__syncthreads();
if (l + 8 < k) {
A += lda << 3;
B += 8;
resA = ((Tv *)A)[x_a + y_a * (lda >> 2)];
resB = ((Tv *)B)[x_b + y_b * (ldb >> 2)];
}
#pragma unroll(4)
for (int j = 0; j < 8; ++j) {
Tv a[2], b[2];
for (int p = 0; p < 2; ++p)
a[p] = ((Tv *)(s_A + (j << 7) + (x_c << 2)))[p << 4];
for (int p = 0; p < 2; ++p)
b[p] = ((Tv *)(s_B + (j << 7) + (y_c << 2)))[p << 4];
for (int p = 0; p < 2; ++p)
for (int q = 0; q < 2; ++q)
for (int i = 0; i < TvSize; ++i)
for (int j = 0; j < TvSize; ++j)
((T *)&ansC[p][q][i])[j] += ((T *)&a[p])[j] * ((T *)&b[q])[i];
}
#if TWO_BUFFER
{
T *tmp_A = s_A;
s_A = s_tA;
s_tA = tmp_A;
}
{
T *tmp_B = s_B;
s_B = s_tB;
s_tB = tmp_B;
}
#else
__syncthreads();
#endif
}
for (int p = 0; p < 2; ++p)
for (int q = 0; q < 2; ++q)
for (int i = 0; i < TvSize; ++i) {
Tv *devC = ((Tv *)(C + ldc * (q * 64 + i))) + (p << 4), resC = *devC;
for (int j = 0; j < TvSize; ++j)
((T *)&resC)[j] =
alpha * ((T *)&ansC[p][q][i])[j] + beta * ((T *)&resC)[j];
*devC = resC;
}
}
}; // namespace wuk
void WuK_Timer(const char *tag, float flo, const std::function<void()> &kernel,
int test_time = 9) {
float min_time = 9e99;
while (test_time--) {
cudaEvent_t beg, end;
cudaEventCreate(&beg);
cudaEventCreate(&end);
cudaEventRecord(beg);
kernel();
cudaEventRecord(end);
cudaEventSynchronize(beg);
cudaEventSynchronize(end);
float elapsed_time;
cudaEventElapsedTime(&elapsed_time, beg, end);
min_time = std::min(min_time, elapsed_time);
}
std::printf("%s: %f ms, %e FLOPS.\n", tag, min_time, flo * 1e3 / min_time);
}
struct WuK_cublas {
cublasHandle_t handle;
WuK_cublas() { cublasCreate(&handle); }
~WuK_cublas() { cublasDestroy(handle); }
} wuk_cublas;
const float alpha = 1, beta = 0;
const cublasOperation_t opA = CUBLAS_OP_N, opB = CUBLAS_OP_N, opC = CUBLAS_OP_N;
const int m = 1 << 13, n = 1 << 13, k = 1 << 13,
lda = opA == CUBLAS_OP_N ? k : m, ldb = opB == CUBLAS_OP_N ? n : k,
ldc = opC == CUBLAS_OP_N ? n : m;
cutlass::HostTensor<float, cutlass::layout::ColumnMajor> dA({m, k}), dB({k, n}),
dC({m, n});
int main() {
cutlass::reference::device::TensorFill(dA.device_view(),
static_cast<float>(2));
cutlass::reference::device::TensorFill(dB.device_view(),
static_cast<float>(1));
cutlass::reference::device::TensorFill(dC.device_view(),
static_cast<float>(0));
WuK_Timer("cublasSgemm", 2.0 * m * k * n, [&] {
cublasSgemm(wuk_cublas.handle, opA, opB, m, n, k, &alpha, dA.device_data(),
lda, dB.device_data(), ldb, &beta, dC.device_data(), ldc);
});
WuK_Timer("CutlassSgemmNN", 2.0 * m * k * n, [&] {
CutlassSgemmNN(m, n, k, alpha, dA.device_data(), lda, dB.device_data(), ldb,
beta, dC.device_data(), ldc);
});
WuK_Timer("Alcanderian::cuda_kernel_sgemm_1", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
Alcanderian::cuda_kernel_sgemm_1<<<gridDim, blockDim>>>(
dA.device_data(), dB.device_data(), dC.device_data(), n, m, k, alpha,
beta);
});
WuK_Timer("Alcanderian::cuda_kernel_sgemm_2", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
Alcanderian::cuda_kernel_sgemm_2<<<gridDim, blockDim>>>(
dA.device_data(), dB.device_data(), dC.device_data(), n, m, k, alpha,
beta);
});
WuK_Timer("Alcanderian::cuda_kernel_sgemm_3", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
Alcanderian::cuda_kernel_sgemm_3<<<gridDim, blockDim>>>(
dA.device_data(), dB.device_data(), dC.device_data(), n, m, k, alpha,
beta);
});
WuK_Timer("fynv::g_fgemm", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 128;
const dim3 blockDim(256), gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m % TILE_WIDTH == 0);
assert(n % TILE_WIDTH == 0);
assert(k % TILE_WIDTH == 0);
fynv::g_fgemm<<<gridDim, blockDim>>>(dC.device_data(), dA.device_data(),
dB.device_data(), k, lda, ldb, ldc);
});
WuK_Timer("wuk::gemm_32x32_v0", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((n + TILE_WIDTH - 1) / TILE_WIDTH,
(m + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= blockDim.y);
assert(n >= blockDim.x);
wuk::gemm_32x32_v0<<<gridDim, blockDim>>>(m, n, k, alpha, dA.device_data(),
lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_32x32_v1", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= blockDim.x);
assert(n >= blockDim.y);
wuk::gemm_32x32_v1<<<gridDim, blockDim>>>(m, n, k, alpha, dA.device_data(),
lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_32x32_v2", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= blockDim.x);
assert(n >= blockDim.y);
wuk::gemm_32x32_v2<<<gridDim, blockDim>>>(m, n, k, alpha, dA.device_data(),
lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_32x32_v3", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= TILE_WIDTH);
assert(n >= TILE_WIDTH);
assert(k >= TILE_WIDTH);
wuk::gemm_32x32_v3<float, TILE_WIDTH><<<gridDim, blockDim>>>(
m, n, k, alpha, dA.device_data(), lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_32x32_v4", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(TILE_WIDTH, TILE_WIDTH),
gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= TILE_WIDTH);
assert(n >= TILE_WIDTH);
assert(k >= TILE_WIDTH);
wuk::gemm_32x32_v4<float, TILE_WIDTH><<<gridDim, blockDim>>>(
m, n, k, alpha, dA.device_data(), lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_32x32_v5", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 32;
const dim3 blockDim(256), gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= TILE_WIDTH);
assert(n >= TILE_WIDTH);
assert(k % 32 == 0);
wuk::gemm_32x32_v5<float, float4, 0><<<gridDim, blockDim>>>(
m, n, k, alpha, dA.device_data(), lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_64x64", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 64;
const dim3 blockDim(256), gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= TILE_WIDTH);
assert(n >= TILE_WIDTH);
assert(k % 16 == 0);
wuk::gemm_64x64<float, float4, 0><<<gridDim, blockDim>>>(
m, n, k, alpha, dA.device_data(), lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
WuK_Timer("wuk::gemm_128x128", 2.0 * m * k * n, [&] {
const int TILE_WIDTH = 128;
const dim3 blockDim(256), gridDim((m + TILE_WIDTH - 1) / TILE_WIDTH,
(n + TILE_WIDTH - 1) / TILE_WIDTH);
assert(opA == CUBLAS_OP_N);
assert(opB == CUBLAS_OP_N);
assert(opC == CUBLAS_OP_N);
assert(m >= TILE_WIDTH);
assert(n >= TILE_WIDTH);
assert(k % 8 == 0);
wuk::gemm_128x128<float, float4, 1><<<gridDim, blockDim>>>(
m, n, k, alpha, dA.device_data(), lda, dB.device_data(), ldb, beta,
dC.device_data(), ldc);
});
}